八大经典排序算法

常见的八种排序算法：插入排序、希尔排序、选择排序、堆排序、冒泡排序、快速排序、归并排序

插入排序

思想：每一步将一个待排序的数据插入到前面已经排好序的有序序列中，直到插完所有元素为止。

当在玩扑克牌整理牌的时候，其实就用到了插入排序的思想。

具体代码实现

void InsertSort(int* const arr, const int len)
{
	assert(arr);
	for (int i = 0; i < len; i++)//遍历每个元素
	{
		for (int j = i; j > 0; j--)//与前面的元素相比较
		{
			if (arr[j] < arr[j - 1])
				swap(arr + j, arr + j - 1);
			else                    //已经有序
				break;
		}
	}
}

复杂度分析：

时间复杂度O(N^2)，空间复杂度O(1)

插入排序是一种稳定的排序算法，当元素集合越接近有序，直接插入排序算法的时间效率越高。

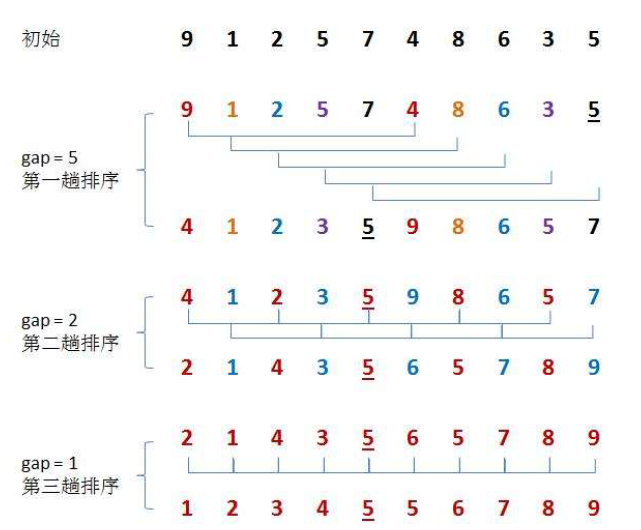
希尔排序

希尔排序也叫缩小增量排序，本质上是对插入排序的优化（利用插入排序当元素集合越接近有序，插入排序算法效率更高的特点）。

思想：对待排序数组中的元素进行分组，从第一个元素开始，按照数组下标中间隔为gap大小的元素分为一组，对每一组进行排序，重新选择gap的大小使得原始数据更加有序，当gap=1的时候就是插入排序。

void ShellSort(int* const arr, const int len)
{
	int gap = len;
	while (gap > 1)
	{
		gap = gap / 3 + 1;//调整gap的大小，gap=1的时候，为插入排序
		for (int i = gap; i < len; i++)//总共只需要循环len-gap次
		{
			for (int j = i; j >= 0; j--)//插入排序
			{
				if (arr[j] < arr[j - gap])
				{
					swap(arr + j, arr + j - gap);
				}
				else
					break;
			}
		}
	}
}

注意：这里的分组比较不是分开进行的（第一组比完第二组在比），而是多组同时进行比较，从第gap个元素开始，逐渐往前比较，每次和自己和自己gap距离的元素比较

复杂度分析：O(N^1.3 - N^2)

稳定性：不稳定

选择排序

思想：每次选择数组元素中最小（最大）的元素放在序列的起始位置，直到全部待排序的数据元素排完。

void SelectSort(int* const arr, const int len)
{
	for (int i = 0; i < len; i++)
	{
		int location = i;//记录最小值的位置
		for (int j = i + 1; j < len; j++)
		{
			if (arr[j] < arr[location])//更新最小值的位置
				location = j;
		}
		if (i != location)
			swap(arr + i, arr + location);
	}
}

复杂度分析：O(N^2)

稳定性：不稳定

堆排序

参考这篇文章

数据结构 - 堆_TangguTae的博客-CSDN博客icon-default.png?t=M1L8https://blog.csdn.net/weixin_43164548/article/details/123149721?spm=1001.2014.3001.5501

冒泡排序

非常经典的排序方法

思想：冒泡排序两两进行比较，遍历完一次都会把最大（小）的元素放在了后面，是一种非常容易理解的排序方法。

void BubbleSort(int* const arr, const int len)
{
	for (int i = 1; i < len; i++)
	{
		for (int j = 0; j < len - i; j++)
		{
			if (arr[j] > arr[j + 1])
			{
				swap(arr + j, arr + j + 1);
			}
		}
	}
}

复杂度分析：O(N^2)

稳定性：稳定

快速排序

非常重要的一个排序，出现的次数超高频！！！

以下方法讨论都是升序场景。

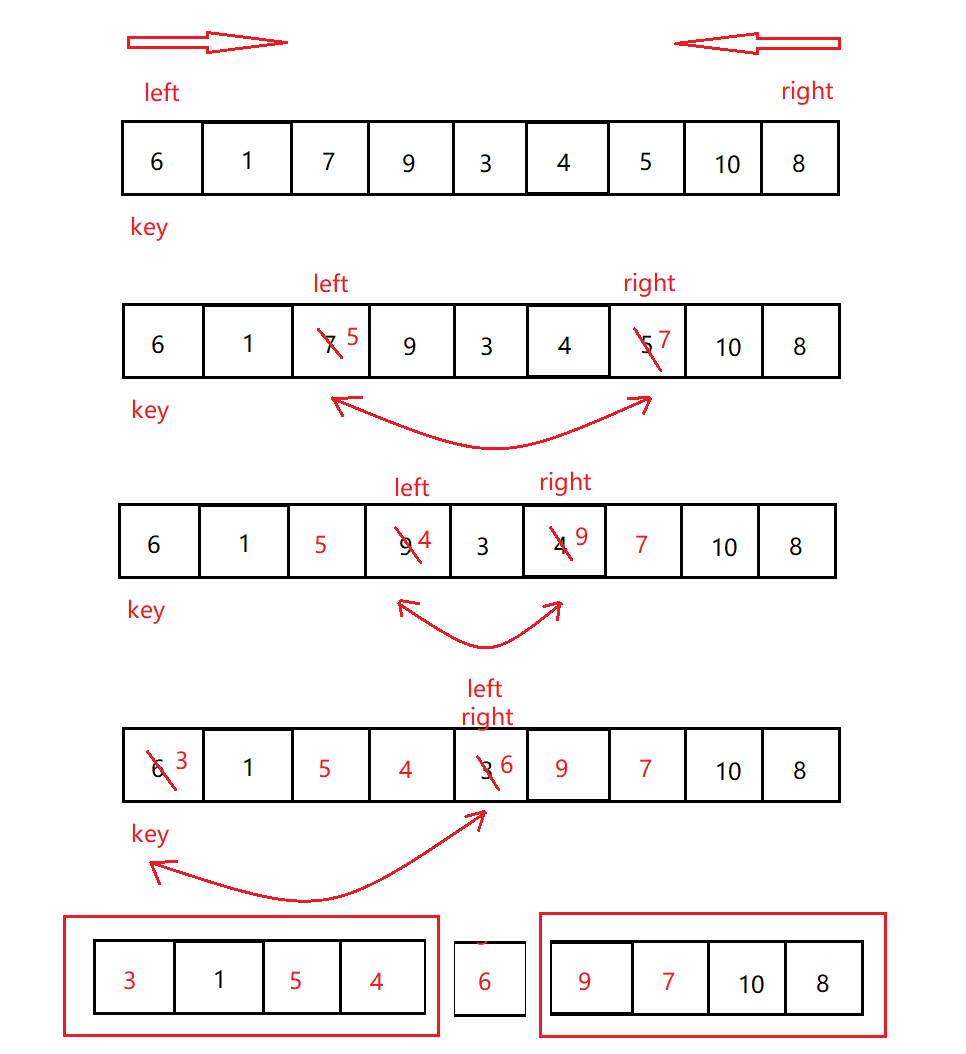
hoare法

思想：利用左右两个下标，分别指向头（left）和尾（right），将数组头部元素设为基准值（key），left往右走寻找比key大的值，right向左走寻找比key小的值（right先出发），双方都找到后交换left和right所指向的数组元素值，直到left和right相遇。相遇后交换key和相遇点的元素值（相遇点一定比key值小，所以需要交换值，原因right先走），这样就可以使得相遇点左边元素都比他小，右边元素都比他大。

void QuickSort(int* const arr, const int begin, const int end)
{
	int left = begin;
	int right = end;
	int key_i = left;
	if (begin >= end)//递归结束条件
		return;

	while (left < right)
	{
		//右边先走
		while (left < right&&arr[right] >= arr[key_i])//找比key_i 处小的值
			right--;
		while (left < right&&arr[left] <= arr[key_i])//找比key_i 处大的值
			left++;
		swap(arr + left, arr + right);
	}
	swap(arr + key_i, arr + left);
	QuickSort(arr, begin, left - 1);//递归
	QuickSort(arr, right + 1, end);
}

复杂度分析：

快速排序的单次排序复杂度为O(N)，最好的情况每次key值都在中间，总共需要递归logN次，所以整体的复杂度为O(NlogN)

最坏的情况是序列为逆序的状态，O(N^2)

稳定性：不稳定

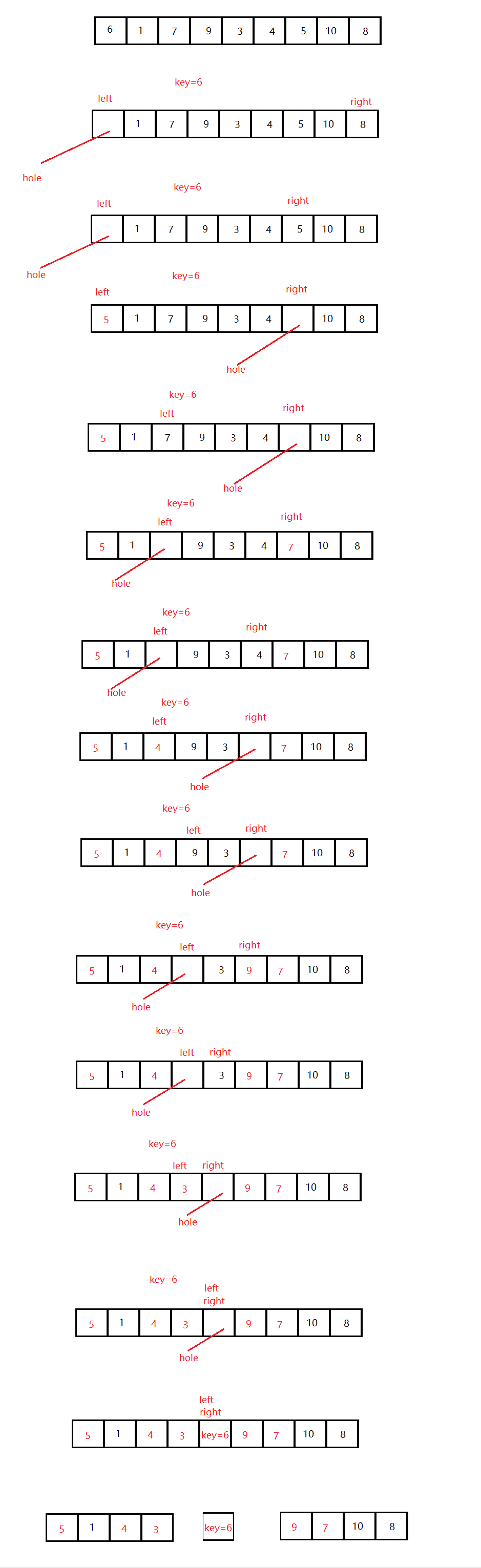
挖坑法

整体思路还是和hoare法类似，需要使得使得相遇点左边元素都比他小，右边元素都比他大（升序）。

思想：假定有一坑hole在序列头部，坑里面的值用key来记录，现在需要把把hole给填上。同样的，先让right往右走，寻找比key值小的元素，找到以后把right里面的值填入坑hole中，这样新的hole就在right这里，然后让left往右走，寻找比key大的值，交换left和hole，直到left和right相遇在hole处，把key值填入hole里。

void QuickSort(int* const arr, const int begin, const int end)
{
	int left = begin;
	int right = end;
	int key = arr[left];
	int hole = left;
	if (begin >= end)
		return;
	while (left < right)
	{
		while (left < right&&arr[right] >= key)//右边先走
			right--;
		arr[hole] = arr[right];//填坑
		hole = right;//更新坑的位置
		while (left < right&&arr[left] <= key)//左边后走
			left++;
		arr[hole] = arr[left];
		hole = left;
	}
	arr[left] = key;
	QuickSort(arr, begin, left - 1);//递归
	QuickSort(arr, right + 1, end);
}

前后指针法

该方法相比较前面两种方法稍微难理解一点，不是很直观。

思想：定义前后两个指针prev和cur，让cur去寻找比key小的值。由于prev在cur的前面，当prev的下一个值不与cur重合时，prev的值与key的值的关系是大于等于（cur已经探寻过了，探寻过的路径只存在比key大的值，除非与prev的下一个重合），交换prev++处与cur处的值。一直迭代，直到cur走到了末尾后，交换prev和key处的值。

void QuickSort(int* const arr, const int begin, const int end)
{
	int prev = begin;
	int cur = begin + 1;
	int key = begin;
	if (begin >= end)
		return;
	while (cur <= end)
	{
		while (cur <= end && arr[cur] > arr[key])//cur去找小于key的值
			cur++;
		if (cur <= end)
		{
			prev++;
			swap(arr + prev, arr + cur);//将prev后一个值与cur处的值交换
			cur++;
		}
	}
	swap(arr + key, arr + prev);
	QuickSort(arr, begin, prev - 1);
	QuickSort(arr, prev + 1, end);
}

快速排序的优化

由于快速排序中key值的大小会影响到整体排序的性能（主要因素），太大或者太小都会影响到快排的效率。递归的深度也会影响到快排的效率，会有较大的开销，可能会栈溢出（次要因素）。

所以可以采取以下两种方法来对快速排序进行优化

1、三数取中

选取头、中、尾三个位置的元素进行比较，选取大小在中间的值，并与首元素进行交换，然后依然按照上面流程继续排序。

目的：这样可以尽可能的避免key值过大或者过小的问题。

int GetMidIndex(int* const arr, int begin, int end)
{
	int mid = (begin + end) >> 1;
	if (arr[begin] > arr[mid])
	{
		if (arr[begin] > arr[end])
		{
			if (arr[mid] > arr[end])
				return mid;
			else
				return end;
		}
		else
			return begin;
	}
	else
	{
		if (arr[begin] < arr[end])
		{
			if (arr[end] > arr[mid])
				return mid;
			else
				return end;
		}
		else
			return begin;
	}
}

所以说对于不同的方法实现的快排，只需要插入两行代码

int MidIndex = GetMidIndex(arr, left, right);//对快排的优化
swap(arr + left, arr + MidIndex);//对快排的优化

2、小区间优化

目的：减少递归的次数

思想：当递归到一定程度时，需要排序的数据量不大，我们可以采用前面所说的插入排序直接完成排序，不需要继续递归下去，数据量少时，反而相比递归效率更高。

对hoare方法优化

void QuickSort(int* const arr, const int begin, const int end)
{
	int left = begin;
	int right = end;
	int key_i = left;
	if (begin >= end)
		return;
	if (end - begin > 10)//假设数据长度小于10就直接采用插入排序，减少递归次数
	{
		while (left < right)
		{
			//右边先走
			while (left < right&&arr[right] >= arr[key_i])
				right--;
			while (left < right&&arr[left] <= arr[key_i])
				left++;
			swap(arr + left, arr + right);
		}
		swap(arr + key_i, arr + left);
		QuickSort(arr, begin, left - 1);
		QuickSort(arr, right + 1, end);
	}
	else
		InsertSort(arr + begin, end - begin + 1);
}

非递归实现快排

非递归实现快排需要借助其他的数据结构来实现。

利用栈来模拟递归的过程。

思路：每次分割序列后，把左右两部分序列的头和尾压入栈中，每次取出头和尾继续分割快排，直到栈中的数据全部取出。

//hoare方法
int QShoareNonR(int* const arr, const int begin, const int end)
{
	int left = begin;
	int right = end;
	int key_i = left;
	while (left < right)
	{
		//右边先走
		while (left < right&&arr[right] >= arr[key_i])
			right--;
		while (left < right&&arr[left] <= arr[key_i])
			left++;
		swap(arr + left, arr + right);
	}
	swap(arr + key_i, arr + left);
	return left;
}
//非递归的逻辑
void QuickSortNon(int* const arr, const int begin, const int end)
{
	std::stack<int> st;
	st.push(begin);
	st.push(end);
	while (!st.empty())//只要栈不为空，继续出栈
	{
        //逻辑：每次把分割后的右边先调整，最后把左边调整
        //注意入栈和出栈的顺序
		int right = st.top();
		st.pop();
		int left = st.top();
		st.pop();
		int meet_i = QShoareNonR(arr, left, right);
		if (meet_i > left)//先入左边，左边最后调整
		{
			st.push(left);
			st.push(meet_i - 1);
		}
		if (meet_i < right)
		{
			st.push(meet_i + 1);
			st.push(right);
		}
	}
}

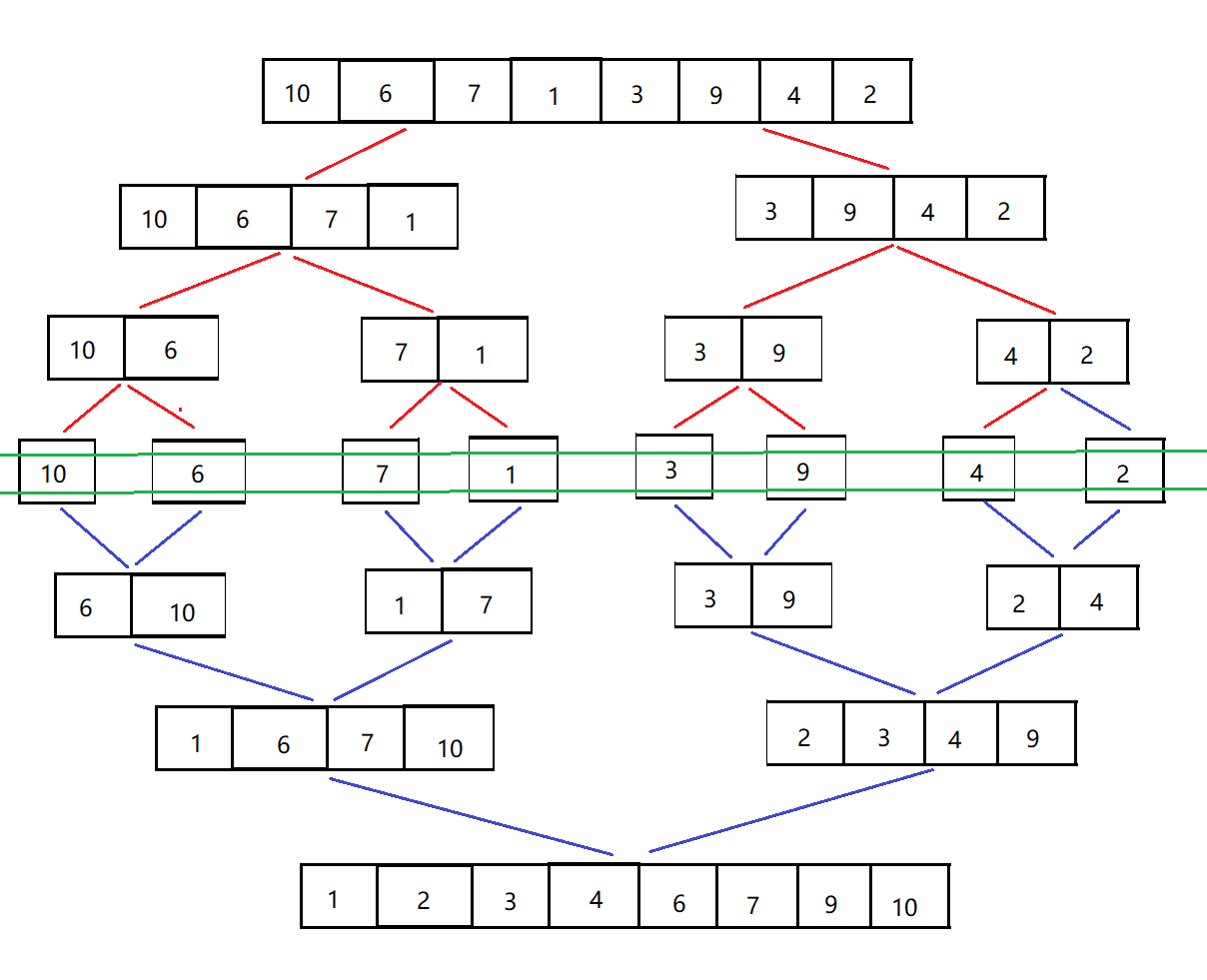
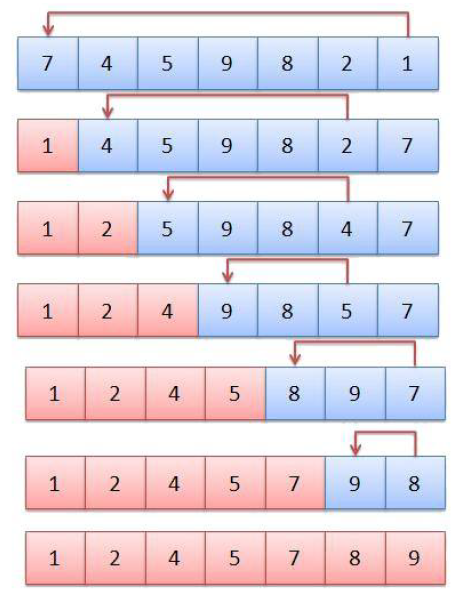
归并排序

归并算法采用非常经典的分治策略，每次把序列分成n/2的长度，将问题分解成小问题，由复杂变简单。

动画演示：

在这里插入图片描述

 原理：先拆分，后合并

具体实现：

void _MergeSort(int* const arr, const int begin, const int end, int* const arr_tmp)
{
	if (begin >= end)
		return;
    //首先先分解问题
	int mid = (begin + end) >> 1;
	_MergeSort(arr, begin, mid, arr_tmp);
	_MergeSort(arr, mid + 1, end, arr_tmp);
    //问题分解完后进行归并
	int head_left = begin;
	int head_right = mid + 1;
	int tmp_index = begin;
	while (head_left<=mid&& head_right<=end)
	{
		if (arr[head_left] < arr[head_right])//对左右两部分进行比较
		{
			arr_tmp[tmp_index++] = arr[head_left++];
		}
		else
		{
			arr_tmp[tmp_index++] = arr[head_right++];
		}
	}
	//剩下的元素直接填充，因为有序
	while (head_left <= mid)
	{
		arr_tmp[tmp_index++] = arr[head_left++];
	}
	while (head_right <= end)
	{
		arr_tmp[tmp_index++] = arr[head_right++];
	}

	//降临时创建的数组的元素拷贝给原数组
	for (int i = begin; i <= end; i++)
	{
		arr[i] = arr_tmp[i];
	}

}
void MergeSort(int* const arr, const int len)
{
	int *arr_tmp = (int*)malloc(sizeof(int)*len);
	_MergeSort(arr, 0, len - 1, arr_tmp);
	free(arr_tmp);
}

复杂度：时间复杂度O(NlogN)，空间复杂度O(1)。

稳定性：稳定

计数排序

本质上是一种映射的思想，和哈希有点类似。

思路：统计数组中每个元素出现的次数，初始化数组中所有元素为0，开辟一个新的数组，把待排序数组中的元素值作为下标，使新的数组在该下标下的值++。在这个统计的过程中，也就相当于对原数组的一个排序过程，统计完之后，按照顺序，出现几次，就在原数组中填几次该元素。

 

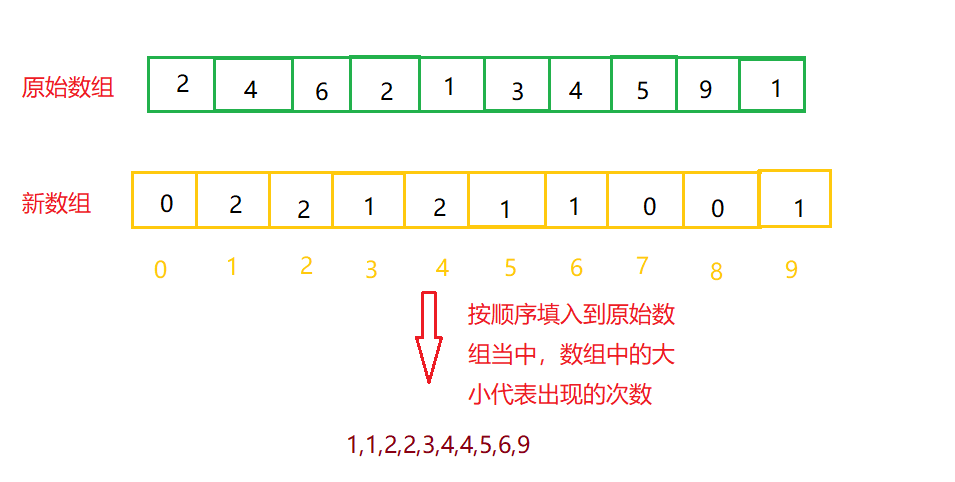
//计数排序
//只能是正整型
void CountSort(int* const arr, int length)
{
	assert(arr);
	//首先寻找最大值和最小值
    //确定新数组的大小
	int max=arr[0], min=arr[0];
	for (int i = 1; i < length; i++)
	{
		if (max < arr[i])
		{
			max = arr[i];
		}
	}
	for (int i = 1; i < length; i++)
	{
		if (min > arr[i])
		{
			min = arr[i];
		}
	}

	int range = max - min + 1;
	int* count = (int*)malloc(sizeof(int)*range);
	memset(count, 0, sizeof(int)*range);//先初始化内存为零
	for (int i = 0; i < length; i++)//统计每个元素出现的次数
	{
		count[arr[i]-min]++;
	}
	int j = 0;
	for (int i = 0; i < range; i++)//根据统计情况，重新覆盖原来数组
	{
		while (count[i]--)
		{
			arr[j++] = min + i;
		}
	}
	free(count);
}

复杂度：时间复杂度O(N+range)，range为待排序序列中最大值与最小值的差值+1；

空间复杂度O(range)。

缺点：只能对正整数进行排序。

正文到此结束
所属分类：Java学习
  • 本文链接： https://refblogs.com/article/200
  • 版权声明： 本文为互联网转载文章，出处已在文章中说明(部分除外)。如果侵权，请联系本站长删除，谢谢。
相关文章
热门推荐
评论插件初始化中...
Loading...
标签云
SQL StringBuffer 工具 比较 LeetCode 程序设计语言 异步通信 社区 嵌套事务 SerializerFeature 常用命令 Future接口 CMD SQL优化 长连接 本地缓存 事务管理 网络安全 简单工厂模式 动画效果 Android 单线程 并发编程 对象 compare lists Caffeine 数据结构 Fetch API 动态伪类 SEO优化 数据过期 软件包管理器 命令 面试 Web开发
本文目录